≪演習1≫
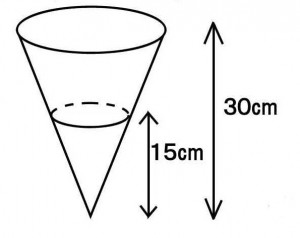
図のような円錐の容器(高さ30cm)に下から15cmまで水をためるのに3分かかった。容器が満水になるのにあと何分かかるか。
1.15分
2.18分
3.21分
4.24分
5.27分
≪正答 3≫
≪演習2≫
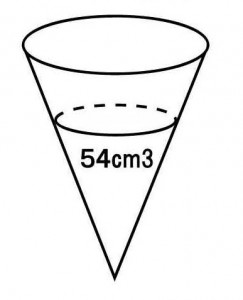
円すい形の容器を頂点を下にして、54cm3の水を入れると容器の高さの3/5まで溜まった。この容器には、あと何cm3の水を入れることができるか。
1.196cm3
2.216cm3
3.256cm3
4.289cm3
5.324cm3
≪正答 1≫
≪演習3≫
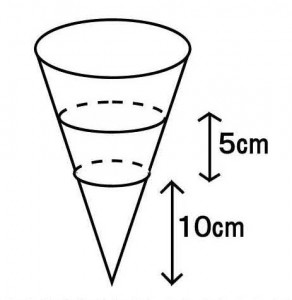
円すい形の容器を頂点を下にして200cm3の水を入れたら、水面の高さが10cmになった。水面をさらに5cm高くするには、何cm3の水を追加すればよいか。
1.400cm3
2.425cm3
3.450cm3
4.475cm3
5.500cm3
≪正答 4≫
≪演習4≫
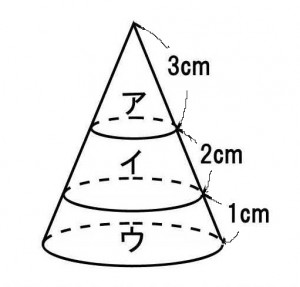
円すいを底面に平行に切って、ア・イ・ウの3つの立体に分けた。イとウの体積比(イ:ウ)はどれか。
1.11:10
2.12:11
3.13:12
4.14:13
5.15:14
≪正答 4≫
≪演習5≫
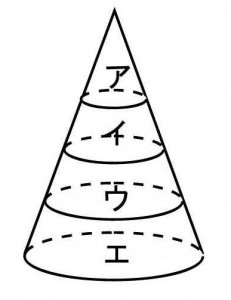
円錐を底面に平行な平面で切って高さの等しい4つの部分に分け、上から順にア・イ・ウ・エとする。(ア+ウ):(イ+エ)の体積比を求めよ。
1.3:7
2.4:9
3.5:11
4.6:13
5.7:15
≪正答 3≫
≪演習6≫
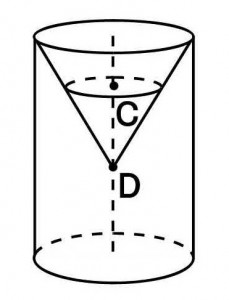
図のような円柱の高さを3等分する点を、C、Dとし、上底面とDを結んで円錐を作った。この円錐を点Cを通り底面に平行に切断した時、大きい方の立体(円錐台)の体積は、円柱全体の体積の何倍か。
1.4/15倍
2.5/18倍
3.6/27倍
4.7/36倍
5.8/49倍
≪正答 4≫
≪演習7≫
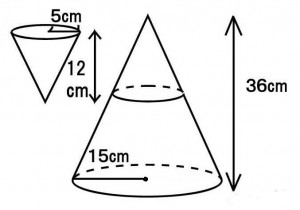
図のような高さが36cmで底面の半径が15cmの円すいを底面に平行な平面で切って小さな円すいと円すい台の2つの容器に分けた。小さい円すいの容器に水を満たし、これを19杯円すい台の容器に注ぐと水面の高さは何cmになるか。
1.12cm
2.15cm
3.16cm
4.19cm
5.20cm
≪正答 1≫
≪演習8≫
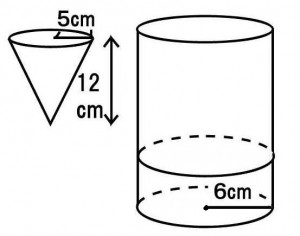
底面の半径が5cmで高さが12cmの円すい形の容器を頂点を下にして水を一杯に満たした。この水を底面の半径が6cmの円柱状の容器に移すと、水の深さは何cmになるか。
1.23/9cm
2.23/8cm
3.25/9cm
4.25/8cm
5.26/9cm
≪正答 3≫
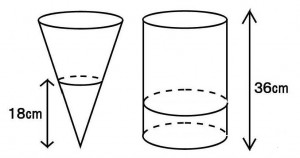
≪演習9≫
同じ底面積をもつ円柱の容器Aと円すいの容器Bがある。AB両方とも空であったが、まず、容器Bを頂点を下にして深さ18cmまで水を入れた。次にそれをすべて容器Aに移すと深さは何cmになるか。ただし、容器Aと容器Bの高さは両方ともに36cmである。
1.1.5cm
2.1.8cm
3.2.0cm
4.2.4cm
5.2.5cm
≪正答 1≫
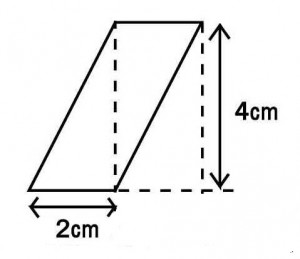
≪演習10≫
底辺2cmで高さ4cmの図のような平行四辺形がある。その内部の2本の対角線のうち短い方の対角線を回転軸として回転させたときにできる立体の体積を求めよ。
1.19/2πc㎡
2.28/3πc㎡
3.37/4πc㎡
4.46/5πc㎡
5.55/6πc㎡
≪正答 2≫