◆解説動画一覧

≪基本１≫
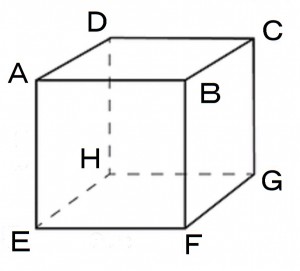
次の立方体を下記の指定した３点を通るように平面で切断したときの切断面の形の名称は何か。

（1）頂点Ａ、Ｃ、Ｆ
（2）頂点Ｆ、辺ＡＢの中点、辺ＢＣの中点

≪基本２≫
上の立方体を下記の指定した３点を通るように平面で切断したときの切断面の形の名称は何か。

（1）頂点Ｄ、Ｆ、辺ＡＥの中点
（2）頂点Ｅ、辺ＡＤの中点、辺ＣＤの中点
（3）辺ＡＤの中点、辺ＣＤの中点、辺ＥＦの中点
（4）頂点Ａ、辺ＣＤの中点、辺ＣＧの中点

≪基本３≫　表切り＆裏切り
次の立方体を頂点ＡとＣとＦの３点を通るように平面で切断したときの切断面の形と同じになる３点指定の切り方はどれか。

１. 頂点Ｄ、Ｅ、Ｇ
２. 頂点D、Ｅ、Ｆ
３. 頂点D、Ａ、Ｆ
４. 頂点Ａ、Ｄ、Ｇ
５. 頂点Ａ、Ｅ、Ｇ

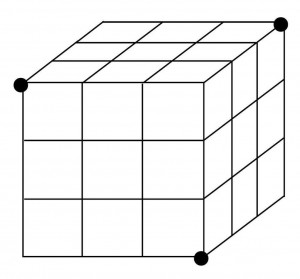
≪基本４≫ ３×３×３
小さな立方体を２７個積み上げて下のような立方体を作った。この立方体の３つの黒丸の頂点を通るように大きな平面で切断したとき、その切断面の名称は何か。また、切断される小さな立方体は何個か。

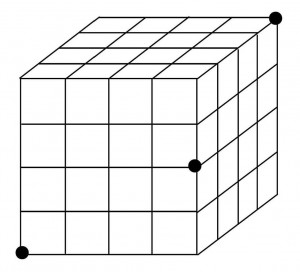
≪基本５≫ ４×４×４
小立方体を６４個を使って作った下図のような立方体がある。この立方体を印をつけた３つの頂点を通るように平面で切断したとき、その切断面の形と切断される小立方体の個数を答えよ。

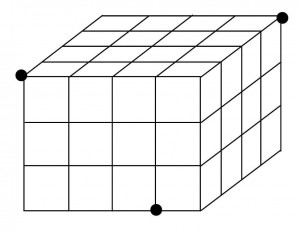
≪基本６≫ ３×４×４
小さな立方体の積み木を、縦４個、横４個、高さ３個になるように積み上げて図のような直方体を作った。この立体上の３点を必ず通るように平面で切断するとき、その切断面の形を考えた上で小さな立方体が何個切断されるか求めよ。

◆解説動画一覧

≪演習１≫
一辺が１０ｃｍの正方形と扇形によってできた下図の斜線部分の面積を求めよ。（円周率は3.14とする）

≪正答 ５７ｃ㎡≫

≪演習２≫
一辺が１０ｃｍの正方形と半円によってできた下図の斜線部分の面積を求めよ。（円周率は3.14とする）

≪正答 ５７ｃ㎡≫

≪演習３≫
一辺が１０ｃｍの正方形と扇形によってできた下図の斜線部分の面積を求めよ。

≪正答 １００－２５ Π ｃ㎡≫

≪演習４≫
半径１０ｃｍの大円の中に図のように４つの小円が重なっておさまっている下図の斜線部分の面積を求めよ。

≪正答 １１４ｃ㎡≫

≪演習５≫
半径２０ｃｍの正方形の中に扇形と半円が描いてある下図の斜線部分の面積を求めよ。

≪正答 １１４ｃ㎡≫

≪演習６≫
半径１０ｃｍの正方形と半円でできた下図の斜線部分の面積を求めよ。（円周率は3.14）

≪正答 ５０ｃ㎡≫

≪演習７≫
直径１２ｃｍの大円の円周上の点Ｂと点Ａを中心として半径６ｃｍの弧を描いた下図の斜線部分の面積を求めよ。但し、弧ＡＢと弧ＡＣの長さは同じとする。

≪正答 ６ Π ｃ㎡≫

≪演習８≫
辺の長さがそれぞれ６ｃｍ、８ｃｍ、１０ｃｍの直角三角形とその辺ＡＢ、辺ＡＣを直径とする半円を描いた下図の斜線部分の面積を求めよ。

≪正答 ２４ｃ㎡≫

≪演習９≫
辺の長さがそれぞれ６ｃｍ、８ｃｍ、１０ｃｍの直角三角形とその辺ＡＢ、辺ＡＣを直径とする半円を描いた下図の斜線部分の面積を求めよ。

≪正答 ２５ Π－２４ ｃ㎡≫

≪演習１０≫
ＡＢ＝２ｃｍ、ＡＣ＝３ｃｍ　の直角三角形の３つの頂点から半径１ｃｍで扇形を描いた下図の斜線部分の面積を求めよ。

≪正答 ３－Π / ２ ｃ㎡≫

≪演習１１≫
正方形の２つの頂点を中心として半径１０ｃｍの扇形を描いた下図の斜線部分の面積を求めよ。

≪正答 ２００－５０ Π ｃ㎡≫

≪演習１２≫
一辺の長さが１２ｃｍの正三角形の辺の中点お中心にして図のように弧を描いたとき、斜線部分の面積を求めよ。

≪正答 １８ Π ｃ㎡≫

≪演習１３≫
一辺が１０ｃｍの正方形の内部に半円の弧を２本描いた下図において斜線部分の面積を求めよ。

≪正答 ５０ｃ㎡≫

≪演習１４≫
縦８ｃｍ、横６ｃｍの長方形の辺ＡＢを直径とする半円がある。この半円を辺ＣＤに向かって弧ＡＢが辺ＣＤに接するまで平行移動させたときに、半円の弧ＡＢが通ったあとの面積を求めよ。

≪正答 １６ｃ㎡≫

≪演習１５≫
半径１２ｃｍで中心角６０度の扇形の中に直角三角形ＡＢＣと直角三角形ＢＤＥが下図のように描かれているとき、斜線部分の面積を求めよ。

≪正答 １２ Π ｃ㎡≫

≪演習１６≫
半径２０ｃｍの扇形の内部に正方形が下図のように描かれていて、その正方形の中に正方形の一辺を半径とする扇形が描かれている。斜線部分の面積を求めよ。

≪正答 ４３ｃ㎡≫

◆解説動画一覧

≪演習１≫
高さ１２ｃｍの円柱形の容器Ａと高さ１０ｃｍの容器Ｂがある。容器Ａに深さ１０ｃｍまで水を入れ、それを容器Ｂにすべて移すと容器Ｂの水位は何ｃｍになるか。但し、容器Ａの底面積は２００ｃ㎡、容器Ｂの底面積は４００ｃ㎡である。

≪正答 ５ｃｍ≫

≪演習２≫
円柱形の容器Ａ，Ｂ，Ｃがある。容器Ａと容器Ｂに同量の水を入れたら容器Ａは１２ｃｍ、容器Ｂは６ｃｍの深さとなった。次にＡとＢの容器に入れた水を全部容器Ｃにいれたら容器Ｃでの水位はいくらか。但し、容器Ｃの底面積の２倍が容器Ａと容器Ｂの底面積の和に等しいとする。

≪正答 １６ｃｍ≫

≪演習３≫
円柱形の容器ＡとＢに同量の水を入れたらＡの水位は８ｃｍ、Ｂの水位は１２ｃｍとなった。このあとＡとＢの水位が等しくなるように水をやり取りした。等しくなったときの水位はいくらか。

≪正答 ９.６ｃｍ≫

≪演習４≫
円筒形の容器Ａ、Ｂ、Ｃに同量の水を入れたら、水の深さがＡは５ｃｍ、Ｂは３ｃｍ、Ｃは２ｃｍとなった。ＡとＢとＣの底面積の比を求めよ。

≪正答 ６：１０：１５≫

≪演習５≫
円筒形の容器Ａ、Ｂ、Ｃがある。最初、容器Ａを満水にした後その１/３を容器Ｃに入れたら容器Ｃの１/２まで入った。次に容器Ａの残りをすべて容器Ｂに移したら、容器Ｂの３/４まで入った。容器Ｂと容器Ｃの底面積の比を求めよ。

≪正答 ４：３≫