≪演習1≫
正十二面体と正二十面体の頂点の数の合計はいくつか。
1.26個
2.28個
3.30個
4.32個
5.34個
≪正答 4 ≫
≪演習2≫
立方体の各面の中心を順に結んで内部に立体Aを作り、次に、立体Aの各面の中心を順に結んでその内部に立体Bを作る。さらに、立体Bの各面の中心を結んで立体Cを作ったとき、立体Cの頂点の数はいくつか。
1.4個
2.6個
3.8個
4.10個
5.12個
≪正答 2 ≫
≪演習3≫
正多面体Aの各面の中心を結んで、その内部に立体を作ったところ、辺の数が12本ある正多面体ができた。正多面体Bの各面の中心を結んで、その内部に立体を作ったところ、辺の数が30本ある正多面体ができた。正多面体Aと正多面体Bの面の数の合計としてありえないのはどれか。
1.18枚
2.20枚
3.24枚
4.26枚
5.28枚
≪正答 3 ≫
≪演習4≫
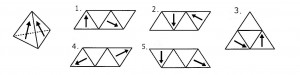
次の図のように、正四面体の2つの面に矢印が書いてある。この正四面体の展開図として正しいものを選べ。
≪正答 5 ≫
≪演習5≫
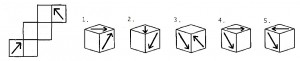
次の図のように、2箇所に矢印が書いてある展開図を組み立てたときにできる立方体の見取り図はどれか。
≪正答 5 ≫
≪演習6≫
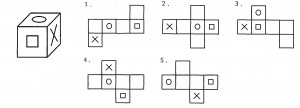
次の図のような見取り図になる正六面体の展開図として正しいものはどれか。
≪正答 5 ≫
≪演習7≫
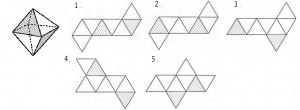
次の図のような見取り図になる正八面体の展開図として正しいものはどれか。
≪正答 2 ≫
≪演習8≫
正六面体の各面の中心を結んでできる立体はある正多面体となるが、その体積は、もとの正六面体の体積の何倍か。
1.1/2
2.1/3
3.1/4
4.1/6
5.1/9
≪正答 4 ≫
≪演習9≫
正四面体の各面の中心を結んで、内部に立体を作るとき、その体積はもとの正四面体の体積の何倍になるか。
1.1/2
2.1/4
3.1/9
4.1/16
5.1/27
≪正答 5 ≫
≪演習10≫
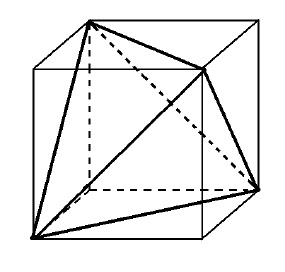
正六面体の内部に、その3つの頂点を3つの角とする三角形によって囲まれた立体を作ると正四面体となるが、その体積はもとの正六面体の体積の何倍か。
1.1/2
2.1/3
3.1/4
4.2/5
5.3/8
≪正答 2 ≫