≪演習1≫
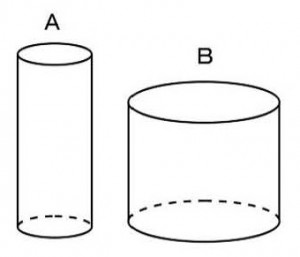
高さ12cmの円柱形の容器Aと高さ10cmの容器Bがある。容器Aに深さ10cmまで水を入れ、それを容器Bにすべて移すと容器Bの水位は何cmになるか。但し、容器Aの底面積は200c㎡、容器Bの底面積は400c㎡である。
≪正答 5cm≫
≪演習2≫
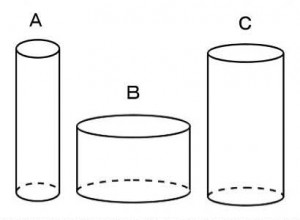
円柱形の容器A,B,Cがある。容器Aと容器Bに同量の水を入れたら容器Aは12cm、容器Bは6cmの深さとなった。次にAとBの容器に入れた水を全部容器Cにいれたら容器Cでの水位はいくらか。但し、容器Cの底面積の2倍が容器Aと容器Bの底面積の和に等しいとする。
≪正答 16cm≫
≪演習3≫
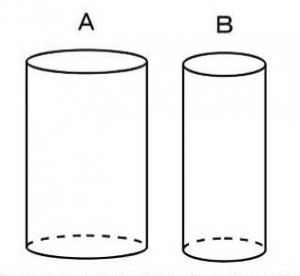
円柱形の容器AとBに同量の水を入れたらAの水位は8cm、Bの水位は12cmとなった。このあとAとBの水位が等しくなるように水をやり取りした。等しくなったときの水位はいくらか。
≪正答 9.6cm≫
≪演習4≫
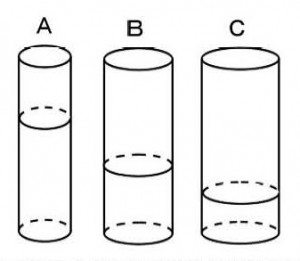
円筒形の容器A、B、Cに同量の水を入れたら、水の深さがAは5cm、Bは3cm、Cは2cmとなった。AとBとCの底面積の比を求めよ。
≪正答 6:10:15≫
≪演習5≫
円筒形の容器A、B、Cがある。最初、容器Aを満水にした後その1/3を容器Cに入れたら容器Cの1/2まで入った。次に容器Aの残りをすべて容器Bに移したら、容器Bの3/4まで入った。容器Bと容器Cの底面積の比を求めよ。
≪正答 4:3≫