≪演習1≫
直径10cmの円Aが直線上のPQ間40πcmを滑らないように転がりながら進むとき、この円Aは何回転するか。
1.1回転
2.2回転
3.3回転
4.4回転
5.5回転
≪正答 4≫
≪演習2≫
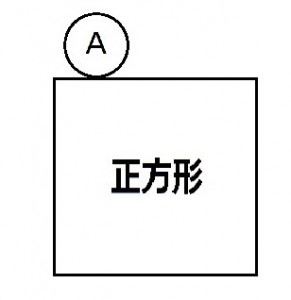
直径10cmの円Aが一辺が10πcmの正方形のまわりを滑らずに転がりながら1周したとき、円Aは何回転したか。
1.1回転
2.2回転
3.3回転
4.4回転
5.5回転
≪正答 5≫
≪演習3≫
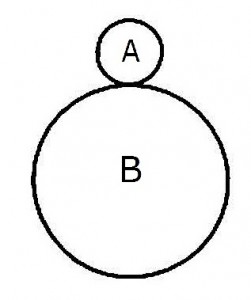
直径6cmの小円Aが直径24cmの大円Bの「外側」を滑ることなく転がりながら1周するとき小円Aは何回転するか。
1.1回転
2.2回転
3.3回転
4.4回転
5.5回転
≪正答 5≫
≪演習4≫
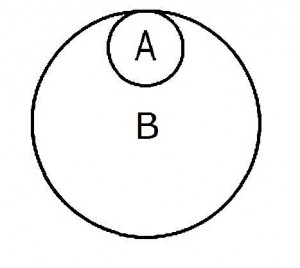
直径6cmの小円Aが直径24cmの大円Bの「内側」を滑ることなく転がりながら1周するとき小円Aは何回転するか。
1.1回転
2.2回転
3.3回転
4.4回転
5.5回転
≪正答 3≫
≪演習5≫
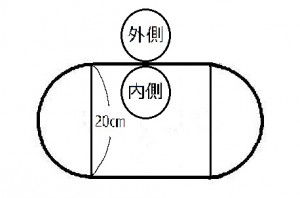
直径10cmの円Aが、長方形と半円2つを組み合わせて作られた図形の外側を滑ることなく回転しながら1周する場合と、同様にして内側を1周する場合の回転数の差は何回か。
1.1回転
2.2回転
3.3回転
4.4回転
5.5回転
≪正答 2≫
≪演習6≫
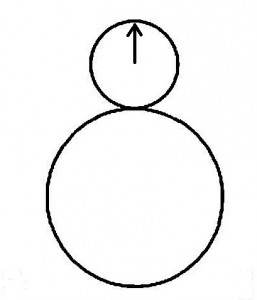
直径10cmの小円板Aが直径25cmの大円板Bの周りを滑らずに回転しながら1周してもとの位置にもどったとき、小円板Aの矢印の方向はどうなるか。(※ただし、転がる前は「もとの位置」において矢印は上↑を向いている)
1.↑
2.←
3.→
4.↓
5.1~4以外の方向
≪正答 4≫
≪演習7≫
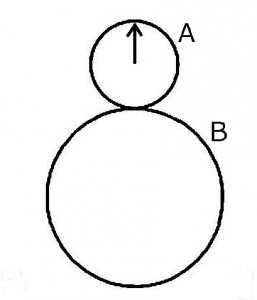
直径15cmの円板Aが直径25cmの円板Bの周りを滑ることなく転がりながら1周してもとの位置にもどってきたとき円板Aの矢印の方向はどうなっているか。(※ただし、転がる前は「もとの位置」において矢印は上↑を向いている)
1.↑
2.←
3.→
4.↓
5.1~4以外の方向
≪正答 5≫
≪演習8≫
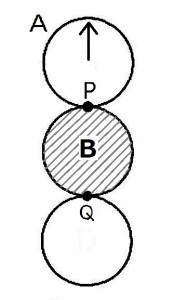
直径8cmの円板Aに図のような方向に矢印をつけて同じ直径8cmの円板Bの周りを滑らないようにPの位置から時計回りに転がしながら1周させた。このとき図のQの位置(真下)では円板Aの矢印はどちらの方向を向いているか。(※ただし、Pは円板Bの12時の位置でQは円板Bの6時の位置とする)
1.↑
2.→
3.←
4.↓
5.1~4以外の方向
≪正答 1≫
≪演習9≫
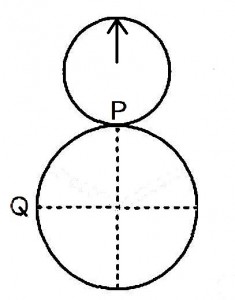
矢印の付いた直径7cmの小円板Aを直径14cmの大円板Bの外側において点Pの位置から滑らないように時計回りの方向に転がした。小円板Aが点Qの位置にきたときの矢印はどちらの方向を向いているか。(※ただし、点Pは大円板Bの12時の位置で、点Qは大円板Bの9時の位置とする)
1.↑
2.→
3.←
4.↓
5.1~4以外の方向
≪正答 2≫
≪演習10≫
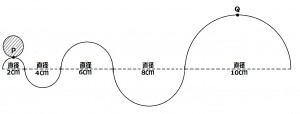
図のように直径の異なる半円(直径2cm、4cm、6cm、8cm、10cm)を組み合わせて作った経路を直径2cmの円Aが滑ることなく点Pから点Qの位置まで転がりながら進むとき、この円Aは何回転するか。
1.4回転
2.4と1/3回転
3.5回転
4.5と1/2回転
5.6回転
≪正答 5≫