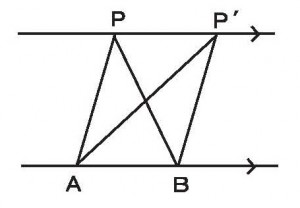
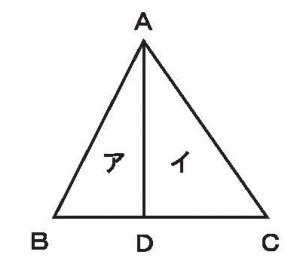
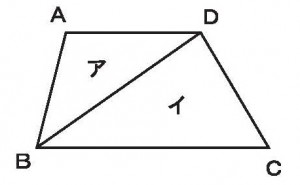
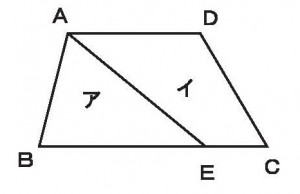
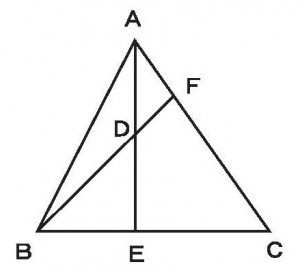
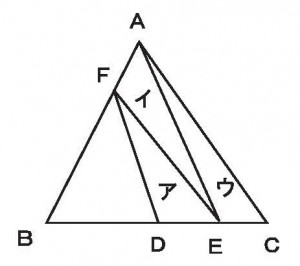
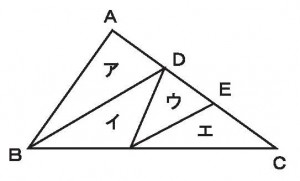
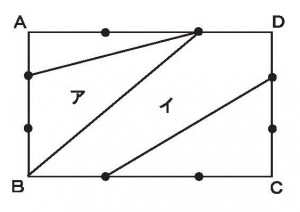
≪基本1≫
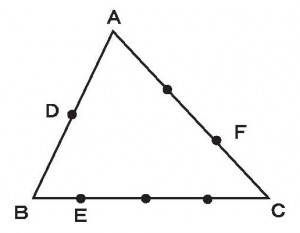
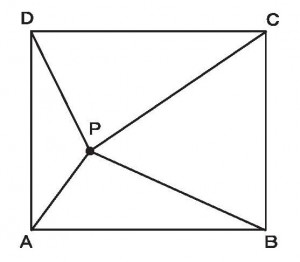
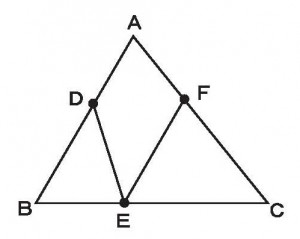
平行線上に頂点を持つ三角形ABPとABP’の面積が等しい理由を述べよ。
≪答 2つの三角形の底辺と高さが等しいから≫
≪基本2≫
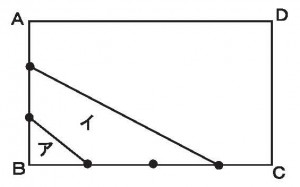
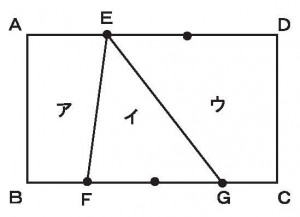
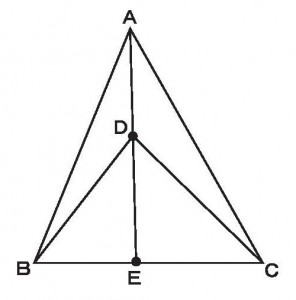
BD=2cm、DC=3cmのとき、2つの三角形アとイの面積の比を求めよ。
≪答 2:3≫
≪基本3≫
下図の台形においてAD=10cm、BC=15cmのとき、三角形アとイの面積比を求めよ。
≪答 2:3≫
≪基本4≫
下図の台形においてAD=10cm、 BE=12cm、EC=4cmのとき、アとイの面積比を求めよ。
≪答 6:7≫
≪基本5≫
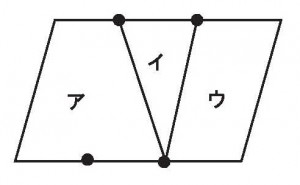
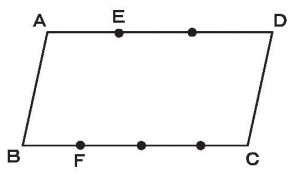
平行四辺形の辺上の三等分点を右のように結んだ。ア:イ:ウ(面積比)を求めよ。
≪答 3:1:2≫
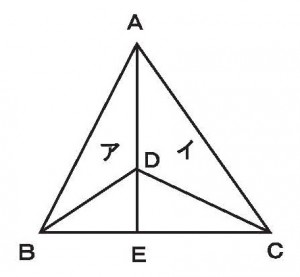
≪基本6≫
AD:DE=3:2、BE:EC=1:2のとき、三角形ADCは三角形ABCのどれだけの割合になるか。(分数で求めよ)
≪答 2/5≫
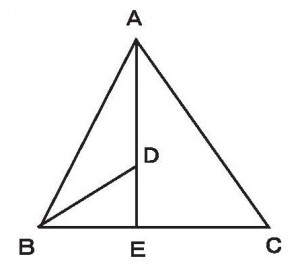
≪基本7≫
点DはAEの内分点(3:2)、点EはBCの内分点(3:4)である。三角形ABDは三角形ABCのどれだけの割合になるか。(分数で求めよ)
≪答 9/35≫
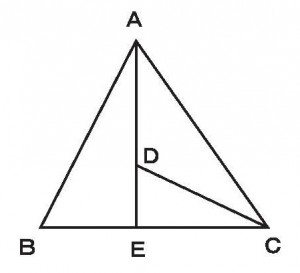
≪基本8≫
点DはAE上の任意の点で、BE:EC=3:5のとき、アとイの面積比を求めよ。
≪答 3:5≫
≪基本9≫
AD:DE=2:3、 BE:EC=1:3のとき、AF:FCを求めよ。
≪答 1:6≫
≪基本10≫
AF:FB=1:2、BD:DE:EC=3:1:1のとき、ア:イ:ウ(面積の比)を求めよ。
≪答 2:4:3≫
≪基本11≫
4つの三角形ア、イ、ウ、工の面積は等しく、AC=12cmのとき、DEは何cmか。
≪答 4.5cm≫
≪基本12≫
三角形ABCの辺ABを4等分、辺BCを3等分した。このとき、点Dと点Eを結んでできる三角形DBEは三角形ABCの何分のいくつか。
≪答 1/6≫
≪基本13≫
三角形ABCの辺ABを2等分、辺BCを4等分、辺ACを3等分したとき、点Dと点Eと点Fを結んでできる三角形DEFは三角形ABCの何分のいくつか。
≪答 7/24≫
≪基本14≫
長方形ABCDの辺ABを3等分、辺BCを4等分して、図のように結んだときアとイの面積の比を求めよ。
≪答 1:5≫
≪基本15≫
平行四辺形ABCDの辺ADを3等分、辺BCを4等分して点Eと点Fを結んだとき、四角形ABFEは平行四辺形ABCDの何分のいくつか。
≪答 7/24 ≫
≪基本16≫
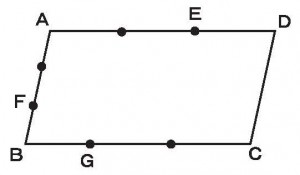
平行四辺形ABCDの辺AB、辺AD、辺BCをそれぞれ3等分した点のうち点Eと点Fと点Gの3点を結んでできた三角形EFGは平行四辺形ABCDの何分のいくつか。
≪答 2/9≫
≪演習1≫
平行四辺形ABCDの辺ADを3等分、辺BCを4等分して点Eと点Fと点Gを右のように結んだ。 アとイとウの面積の比を求めよ。
1.7:6:10
2.7:6:11
3.7:6:12
4.8:7:11
5.8:7:12
≪正答 2≫
≪演習2≫
長方形ABCDの内部に点Pをとり4つの三角形を作ったとき、三角形APD=286cm2、三角形ABP=310cm2、三角形DPC=651cm2となった。三角形BCPの面積はいくらか。
1.675cm2
2.679cm2
3.683cm2
4.687cm2
5.691cm2
≪正答 1≫
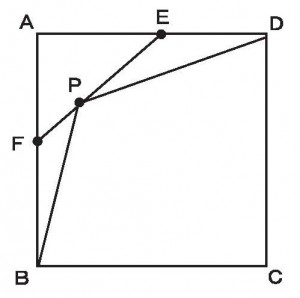
≪演習3≫
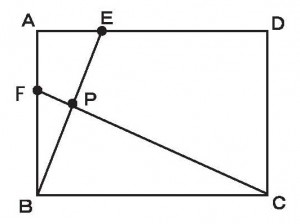
一辺が14cmの正方形ABCDの辺AD上に2等分点Eをとり、辺AB上に2等分点Fをとる。次に線分EF上に任意の点Pをとって点Bと点Dを結び四角形BCDPを作った。このとき四角形BCDPの面積を求めよ。
1.129cm2
2.138cm2
3.147cm2
4.156cm2
5.165cm2
≪正答 3≫
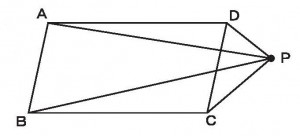
≪演習4≫
下図において四角形ABCDが平行四辺形であるとき、三角形ABPと三角形DCPの面積の差を求めよ。ただし、AD=20cm、ADとBCの距離(平行四辺形の高さ)は15cmとする。
1.110cm²
2.120cm²
3.130cm²
4.140cm²
5.150cm²
≪演習5≫
AD:DB=2:3、AF:FC=4:5で三角形DBEと四角形ADEFの面積の比は1:2である。このときBEとECの長さの比を求めよ。
1.2:3
2.3:5
3.4:7
4.5:9
5.6:11
≪正答 4≫
≪演習6≫
BE:EC=4:5、AD:DE=2:3のとき、三角形ABDと三角形DECの面積の比を求めよ。
1.4:7
2.5:9
3.6:11
4.7:13
5.8:15
≪正答 5≫
≪演習7≫
長方形ABCDにおいて、AE=10cm、ED=30cm、AF=9cm、FB=12cmとする。このときFPとPCの長さの比を求めよ。
1.1:5
2.1:6
3.1:7
4.2:5
5.2:7
≪正答 3≫
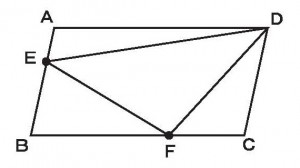
≪演習8≫
下の図の平行四辺形ABCDの面積が48cm2のとき、三角形DEFの面積を求めよ。ただし、AE:EB=1:2、BF:FC=3:1とする。
1.18cm2
2.20cm2
3.22cm2
4.24cm2
5.26cm2
≪正答 3≫
≪演習9≫
長方形ABCD各辺に3等分点をとり、図のように結んだときアとイの面積の比を求めよ。
1.1:2
2.1:3
3.2:3
4.2:5
5.3:5
≪正答 1≫
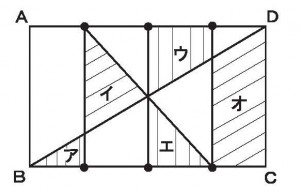
≪演習10≫
長方形ABCDの辺ADと辺BCをそれぞれ4等分した各点と頂点B及びDを右図のように結んだとき、(ア+イ):(ウ+エ+オ)の面積の比を求めよ。
1.1:3
2.2:5
3.3:7
4.4:9
5.5:11
≪正答 1≫