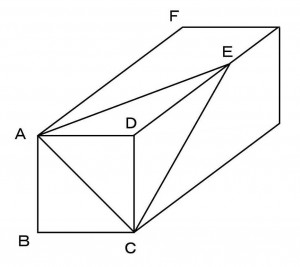
≪演習1≫
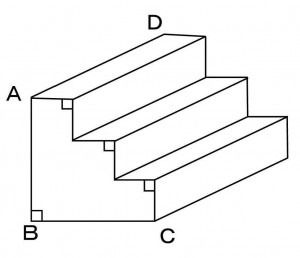
下図の階段状の立体についてAB=BC=30cmで、AD=20cmならば、この立体の体積はいくらか。
≪正答 12000 cm3 ≫
≪演習2≫
上記立体の表面積はいくらか。
≪正答 3600 cm2 ≫
≪演習3≫
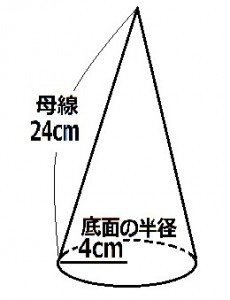
母線24cmで底面の半径が4cmの円錐の展開図において側面積(おうぎ形)の中心角は何度か。
≪正答 60度 ・ 96 Π cm2 ≫
≪演習4≫
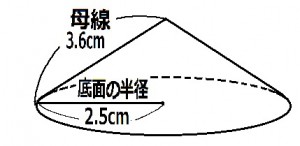
母線の長さが3.6cmで底面の半径が2.5cmの円錐の表面積はいくらか。
≪正答 9 Π cm2 ≫
≪演習5≫
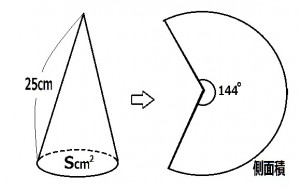
母線の長さが25cmでその展開図の側面積(おうぎ形)の中心角が144度の円錐の底面(円)の面積を求めよ。
≪正答 100 Π cm2 ≫
≪演習6≫
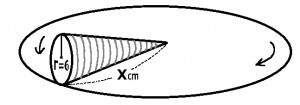
底面の半径が6cmの円錐を横に倒して机の上で頂点を中心に転がしたら、机の上で円を1周描いてもとの位置に戻ったとき、この円錐はちょうど5回転していた。この円錐の母線の長さを求めよ。
≪正答 30cm ≫
≪演習7≫
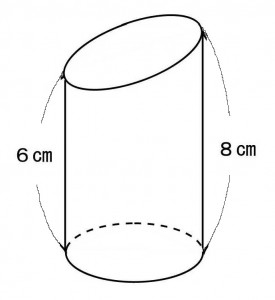
下図の立体は底面の半径が2cmの円柱を斜めに切ったものである。この立体の体積を求めよ。
≪正答 28 Π cm3 ≫
≪演習8≫
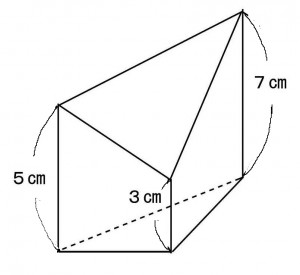
右図は底面の三角形の面積が10c㎡の三角柱を斜めに切ったものである。この立体の体積を求めよ。
≪正答 50cm3 ≫
≪演習9≫
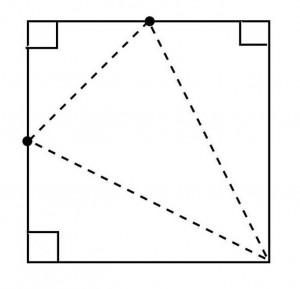
一辺の長さが8cmの正方形の紙を使って、右図のように2辺のそれぞれの中点と1つの頂点を結ぶ線で折り曲げて三角柱を作るとき、この三角柱の体積を求めよ。
≪正答 64/3cm3 ≫
≪演習10≫
右図の直方体においてABCDは一辺が4cmの正方形で、AF=9.6cm、DE=7.2cmである。この直方体を点A,C,Eを通る平面で2つの立体に切り分けたとき、大きい方と小さい方の立体の体積比を求めよ。
≪正答 7:1≫