≪演習1≫
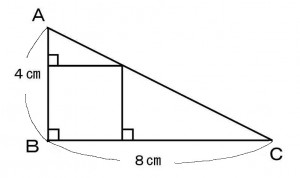
直角三角形ABCの内部の下図のようにおさまった正方形の面積を求めよ。
1. 64/7 c㎡
2. 8 c㎡
3. 64/9 c㎡
4. 7 c㎡
5. 64/11 c㎡
≪正答 3≫
≪演習2≫
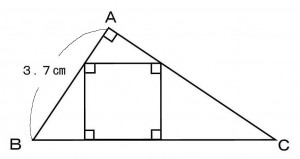
直角三角形ABCの内部の下図のようにおさまった正方形の面積を求めよ。
1. 3c㎡
2. 3.3c㎡
3. 3.5c㎡
4. 3.7c㎡
5. 4c㎡
≪正答 5≫
≪演習3≫
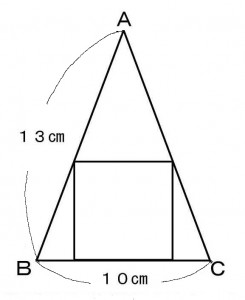
AB=AC=12cmの二等辺三角形ABCの内部の下図のようにおさまった正方形の一辺の長さを求めよ。
1. 60/11cm
2. 60/13cm
3. 60/17cm
4. 70/11cm
5. 70/13cm
≪正答 1≫
≪演習4≫
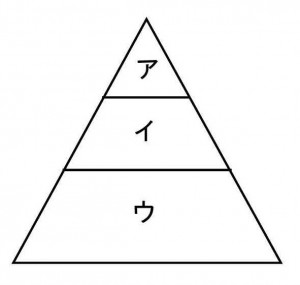
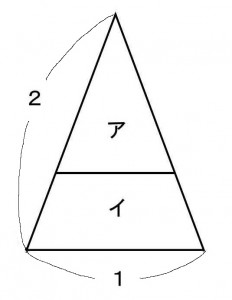
三角形を2本の平行な線分で下図のようにア、イ、ウの3つの図形に切り分けたら、この3つの図形の面積の比が、ア:イ:ウ=4:5:16 となった。このとき切り分けられた3つの図形の周りの長さの比を求めよ。
1. 4:5:16
2. 5:6:14
3. 6:7:12
4. 7:8:15
5. 8:9:17
≪正答 3≫
≪演習5≫
大きな三角形を1本の線分で三角形アと台形イに分けたところアとイの周りの長さが等しくなった。アとイの面積の比を求めよ。
1. 12:13
2. 13:16
3. 16:25
4. 25:39
5. 32:49
≪正答 4≫
≪演習6≫
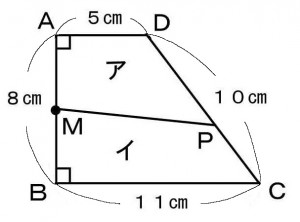
下図のような台形を辺ABの中点Mから辺DCに引いたMPによって2つの四角形アとイに分けたところアとイの面積が等しくなった。PCの長さを求めよ。
1. 25/8 cm
2. 26/9 cm
3. 27/8 cm
4. 28/9 cm
5. 29/8 cm
≪正答 1≫
≪演習7≫
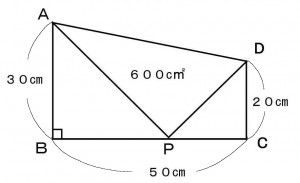
下図のような台形ABCDの辺BC上に点Pをとり点Aと点Bと結んだところ三角形APDの面積が600c㎡になった。このとき辺PCの長さを求めよ。
1. 15cm
2. 18cm
3. 20cm
4. 21cm
5. 24cm
≪正答 3≫
≪演習8≫
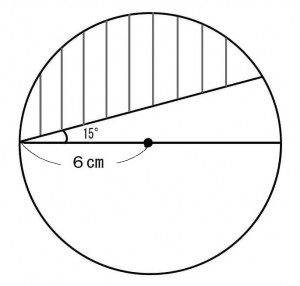
半径6cmの円の内部に下図のように円周の2点を結ぶ線を引いた。このとき斜線部分の面積を求めよ。
1. 15π-1 c㎡
2. 15π-3 c㎡
3. 15π-5 c㎡
4. 15π-7 c㎡
5. 15π-9 c㎡
≪正答 5≫
≪演習9≫
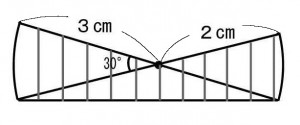
下図は中心角30度で半径3cmと半径2cmの扇形と三角形を組み合わせた図形である。図形全体(斜線部分)の面積を求めよ。
1. 11/12π+3/2 c㎡
2. 13/12π+3/2 c㎡
3. 17/12π+3/2 c㎡
4. 19/12π+3/2 c㎡
5. 23/12π+3/2 c㎡
≪正答 2≫
≪演習10≫
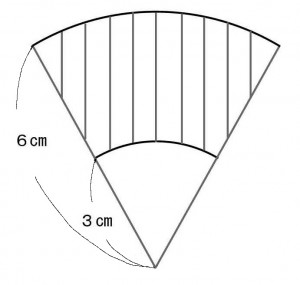
下図は中心角が等しい半径3cmと半径6cmの扇形を重ねた図形である。斜線部分の周りの長さが27cmのとき斜線部分の面積を求めよ。
1. 9π+1c㎡
2. 10π c㎡
3. 31.5 c㎡
4. 10π+1 c㎡
5. 32.5 c㎡
≪正答 3≫