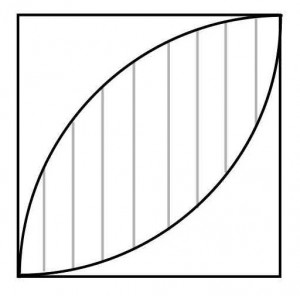
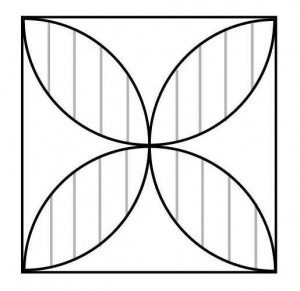
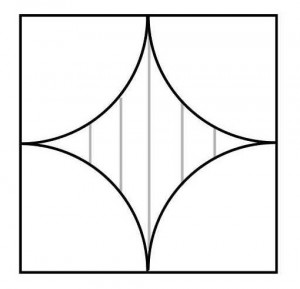
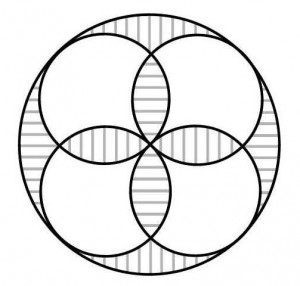
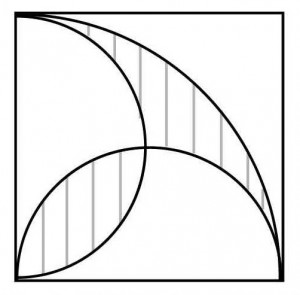
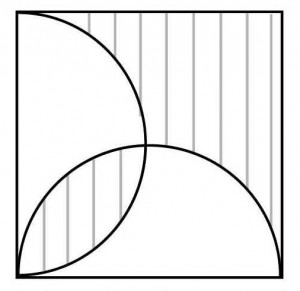
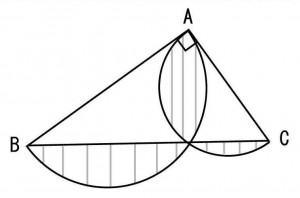
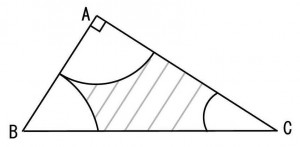
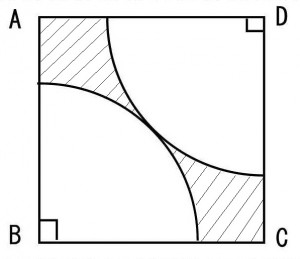
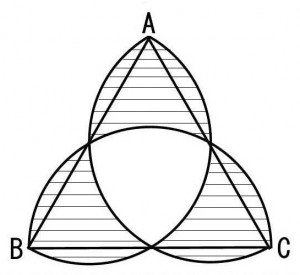
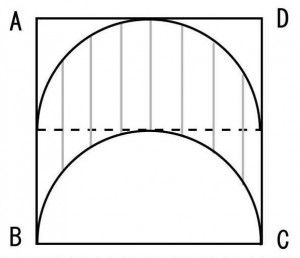
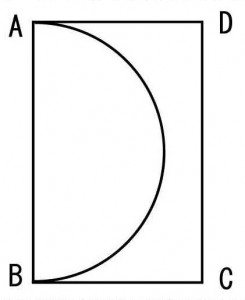
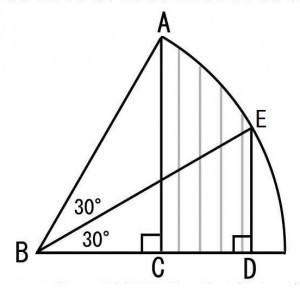
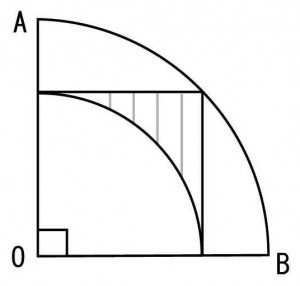
≪演習1≫
一辺が10cmの正方形と扇形によってできた下図の斜線部分の面積を求めよ。(円周率は3.14とする)
≪正答 57c㎡≫
≪演習2≫
一辺が10cmの正方形と半円によってできた下図の斜線部分の面積を求めよ。(円周率は3.14とする)
≪正答 57c㎡≫
≪演習3≫
一辺が10cmの正方形と扇形によってできた下図の斜線部分の面積を求めよ。
≪正答 100-25 Π c㎡≫
≪演習4≫
半径10cmの大円の中に図のように4つの小円が重なっておさまっている下図の斜線部分の面積を求めよ。
≪正答 114c㎡≫
≪演習5≫
半径20cmの正方形の中に扇形と半円が描いてある下図の斜線部分の面積を求めよ。
≪正答 114c㎡≫
≪演習6≫
半径10cmの正方形と半円でできた下図の斜線部分の面積を求めよ。(円周率は3.14)
≪正答 50c㎡≫
≪演習7≫
直径12cmの大円の円周上の点Bと点Aを中心として半径6cmの弧を描いた下図の斜線部分の面積を求めよ。但し、弧ABと弧ACの長さは同じとする。
≪正答 6 Π c㎡≫
≪演習8≫ ※YouTubeの動画解説はありません。
辺の長さがそれぞれ6cm、8cm、10cmの直角三角形とその辺AB、辺ACを直径とする半円を描いた下図の斜線部分の面積を求めよ。
≪正答 24c㎡≫
≪演習9≫ ※YouTubeの動画解説はありません。
辺の長さがそれぞれ6cm、8cm、10cmの直角三角形とその辺AB、辺ACを直径とする半円を描いた下図の斜線部分の面積を求めよ。
≪正答 12.5 Π-24 c㎡≫
≪演習10≫
AB=2cm、AC=3cm の直角三角形の3つの頂点から半径1cmで扇形を描いた下図の斜線部分の面積を求めよ。
≪正答 3-Π / 2 c㎡≫
≪演習11≫
正方形の2つの頂点を中心として半径10cmの扇形を描いた下図の斜線部分の面積を求めよ。
≪正答 200-50 Π c㎡≫
≪演習12≫
一辺の長さが12cmの正三角形の辺の中点お中心にして図のように弧を描いたとき、斜線部分の面積を求めよ。
≪正答 18 Π c㎡≫
≪演習13≫
一辺が10cmの正方形の内部に半円の弧を2本描いた下図において斜線部分の面積を求めよ。
≪正答 50c㎡≫
≪演習14≫
縦8cm、横6cmの長方形の辺ABを直径とする半円がある。この半円を辺CDに向かって弧ABが辺CDに接するまで平行移動させたときに、半円の弧ABが通ったあとの面積を求めよ。
≪正答 16c㎡≫
≪演習15≫
半径12cmで中心角60度の扇形の中に直角三角形ABCと直角三角形BDEが下図のように描かれているとき、斜線部分の面積を求めよ。
≪正答 12 Π c㎡≫
≪演習16≫
半径20cmの扇形の内部に正方形が下図のように描かれていて、その正方形の中に正方形の一辺を半径とする扇形が描かれている。斜線部分の面積を求めよ。
≪正答 43c㎡≫